其实这个问题困扰我很长一段时间,相信有很多朋友也会遇到同样的困惑:如果让自己的钢笔画出流畅的线条?(其实这个问题并不止困扰设计师,几百年就有偏执的家伙研究过这个课题,有兴趣的同学可以了解下马库斯·汤普森Marcus Thompson)
通常,所有二维软件里所有绘制曲线的方法都是基于贝塞尔数学模型,就是通过两个锚点来确定一要线, 并且每个锚点都有两个控制顶点。 通过拉动这些顶点来精确控制曲线的走向以及弧度。简而言之,如果对点的控制得心应手就相当于对线的弧度得心应手。 相此可以推断:要对所有的点控制好,首先要保证你的曲线里点的数量保持在最少!
为什么我要强调锚点数量呢,很多小伙伴们画一段简单的曲线大约有下面这两种方式:
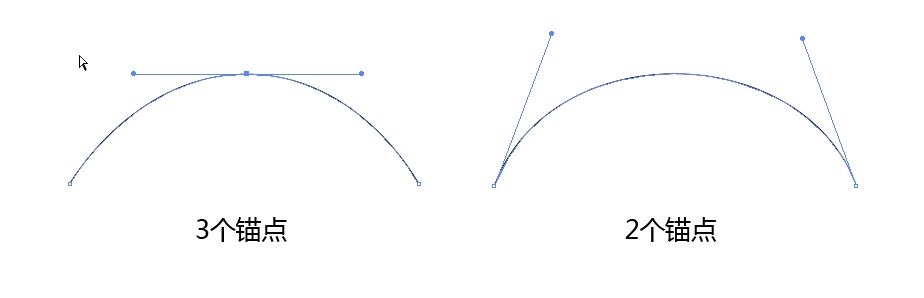
也许你要说多一个锚点没有任何关系,那接下来我们看看这种情况:

对于一条不流畅的曲线来说,造成它生硬的原因就是有太多控制柄在扰乱它的走向,再加上主人对描点的控制不够,而且使用大量不必要的描点会使你的工作难度(你要控制的手柄数量)程指数级上升!
那么我们解决问题的核心就明了了: 关键在如何把复杂的曲线拆分为你可以控制好的【两点一线】
通常最基本的两个锚点可以组成两种形态的曲线,一种是“C”型,一种是“S”型(“乙”型可以看作是“c”型加一条直线 ,只要把锚点一端的手柄去掉即可)。我们的重心就从如何画曲线转移到了如何拆分曲线上(什么?你连自己要画的logo草图都没有? 往前翻翻我写的设计师的高效工作流程去!)。 比如我们要画一个最简单的心型:
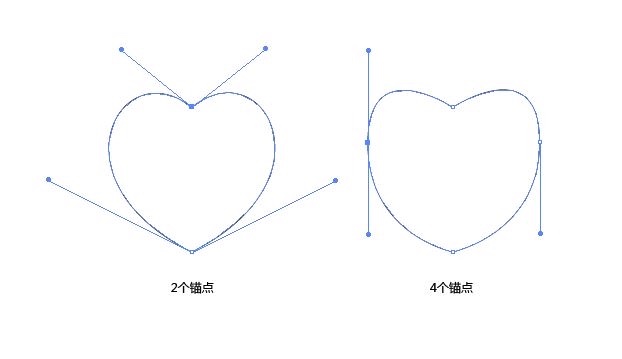
可以很明显的发现,两个锚点的版本更流畅优美。当然四个锚点经过细心的调整也可以达到这样的程度,但是无论在操控上还是时间上都是都极没有性价比的一种做法。所以,下次当你们拿到一个形状,你看到的都是“C”型与“S”型就对了。另:注意好手柄的长度与及夹角。
——————绝望的分割线–2013.9.28晚————————————————————————
我发现,两个锚点根本无法画出所有弧度的“S”型曲线,最简单的应证就是:在某一些看上去很流畅的s型曲线你觉得很容易用两个锚点画出来,但实际上–不能。 不信的话你可以随意打一个“s”字母,并在ai里用两个锚点重绘出来,你会发现大部分情况下是不可能100%重合的。 更绝望的是,C型曲线也一样,不可能用两个锚点画出所有的C(你会发现画一个标准的圆默认有4个锚点,而按照我上面写的推论2个锚点就可以画出正圆)。 如果这两个推论不成立,那么我上面写的都是p话(无法用一个统一的基本规律去应对所有的情况)。待我明天去解决这个问题。
——————纠结的分割线–2013.9.30—————————————————————————
我们先从最基本的 C 型曲线开始。
要确定两个锚点可以画哪个范围内的『流畅的C 型曲线』,那我们就要确定什么样的曲线才算是『流畅』这个问题。 我认为:一个标准的正圆和羊角曲线模型都可以算是标准的『流畅』。
下面我们画一个正圆,很容易发现系统默认用4个点来构成这个圆,为什么要 4 个点?我们试试减少锚点的数量:

这两个圆可以完全重合, 也就是说,一个正圆是可以由三个锚点来完成。于是我再次尝试用两个锚点来完成这个圆,结果毫无疑问是失败。 于是我便退而求其次用两个点来描绘大于120度的弧线 , 起初误差还不是很大,随着角度的变大,差值也就越大。
结论:弧度夹角在120度以内的曲线,可以用两个锚点完美的绘制, 当它超过120度,两个锚点就无能为力。
下面是羊角曲线:
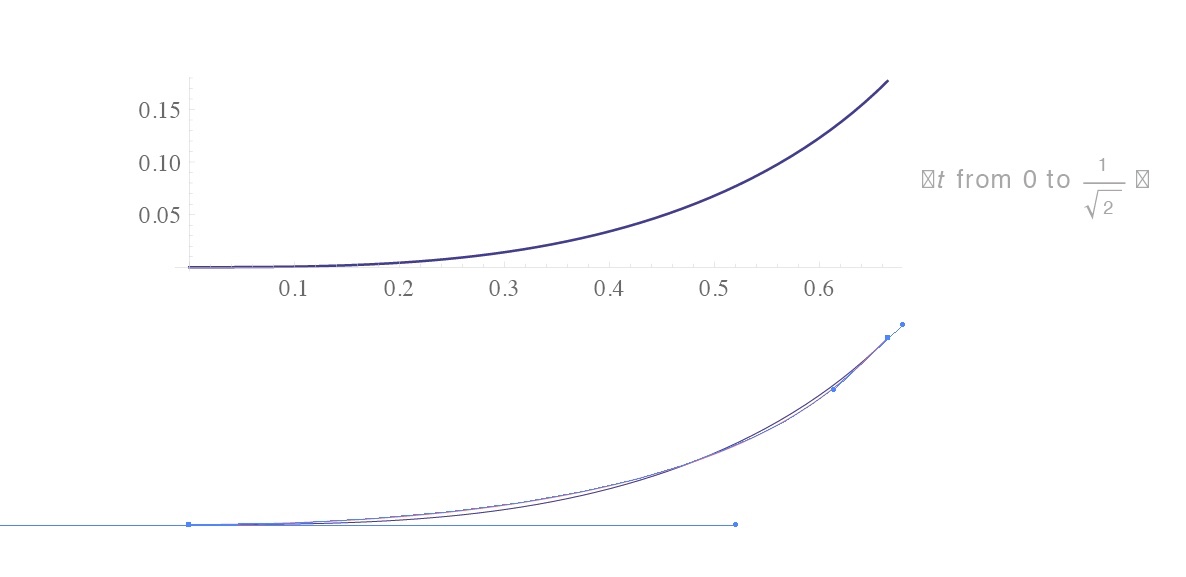
这个就更坑爹了有没有? 由于羊角曲线的曲率不定,几乎无法用两个锚点来重合它稍稍大一点的角度(目测不会超过30度)。这种复杂性让我不得不开始反思:我们需要如此精确的『流畅性』么?毕竟 adobe 也没有用极致的3个锚点去绘制一个正圆?难道是纯粹的为了对称或者是为了便于修改?
上面研究了C型的曲线 ,貌似S型曲线的适用范围更窄. 我用过两个圆相切,得到一段光滑的曲线,发现两个锚点连最基础的两段90度夹角的C弧连起来的S型都无法绘制出来。 经过不断尝试,相信大家也猜到了,它只能绘制出两段60度以内的C型弧连起来的S型。 60+60=120.尼马数学真是一门神奇又而精确的学问。
终极结论: 尽可能地控制锚点的数量,并且训练自己对锚点位置的排布能力,C型与S型曲线的作用范围。